Diagonal Difference

• Diagonal Difference on HackerRank

This is a classic matrix problem. The “diagonal difference” is just the easy part (a subtraction). The main challenge here is to sum the diagonals of the given square matrix.

1     2     3

4     5     6

7     8     9

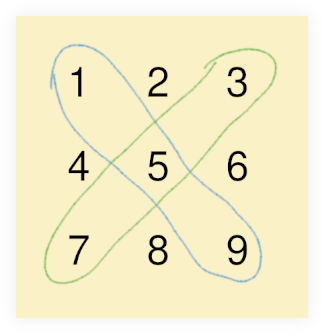
Basically, our goal is to sum 1, 5 and 9 from the right to left diagonal, 3, 5 and 7 from the left to right diagonal, and perform the subtraction.

JavaScript

Solution 1 with nested loops

/**
 * Calculates the diagonal difference of the square matrix.
 *
 * T.C: O(n²).
 * S.C: O(1).
 *
 * @sig [Number] -> Number
 */
function diagDiff(sqrMatrix) {
  const len = sqrMatrix.length;
  let ltrDiag = 0;
  let rtlDiag = 0;

  for (let i = 0; i < len; i++) {
    for (let j = 0; j < len; j++) {
      if (i === j)
        ltrDiag += sqrMatrix[i][j];

      if (i + j === len - 1)
        rtlDiag += sqrMatrix[i][j];
    }
  }

  return Math.abs(ltrDiag - rtlDiag);
};

The time complexity is \(O(n^2)\) because of the nested looping.

Solution 2 with single loop

/**
 * Calculates the diagonal difference of the square matrix.
 *
 * - T.C: O(n).
 * - S.C: O(1).
 *
 * @sig [Number] -> Number
 */
function diagDiff(xs) {
  let ltrDiag = 0;
  let rtlDiag = 0;
  let len = xs.length;

  for (let i = 0; i < len; ++i) {
    ltrDiag += xs[i][i];
    rtlDiag += xs[i][len - i - 1];
  }

  return Math.abs(ltrDiag - rtlDiag);
}

With this implementation, the time complexity is \(O(n)\) (not \(O(n²)\) like in the previous solution) because the sum of the left and right diagonals are calculated within the same loop.

A combination of i and len is used so that indices are accessed from the left and right at the same time. Because of len - i, each time i is incremented by the loop, that len - i produces lower and lower indexes each time.

That len - 1 - 1 can be simplified a little bit:

/**
 * Calculates the diagonal difference of the square matrix.
 *
 * - T.C: O(n).
 * - S.C: O(1).
 *
 * @sig [Number] -> Number
 */
function diagDiff(xs) {
  let ltrDiag = 0;
  let rtlDiag = 0;
-  let len = xs.length;
+  const lastPos = xs.length - 1;

  for (let i = 0; i < len; ++i) {
    ltrDiag += xs[i][i];
-    rtlDiag += xs[i][len - i - 1];
+    rtlDiag += xs[i][lastPos - i];
  }

  return Math.abs(ltrDiag - rtlDiag);
}