ch09 Exercises :: Lists¶
We can insert ⊥ (bottom) on Linux Gtk with Ctrl+Shift+U followed by 22a5.
On Vim, in insert mode with Ctrl+v u 22a5.
On Emacs with C-x u RET 22a5 RET.
Will it blow up?¶
Will the expressions return a value or ⊥ (bottom)?
1. [x^y | x <- [1..5], y <- [2, undefined]]
2. take 1 $ [x^y | x <- [1..5], y <- [2, undefined]]
3. sum [1, undefined, 3]
4. length [1, 2, undefined]
5. length $ [1, 2, 3] ++ undefined
6. take 1 $ filter even [1, 2, 3, undefined]
7. take 1 $ filter even [1, 3, undefined]
8. take 1 $ filter odd [1, 3, undefined]
9. take 2 $ filter odd [1, 3, undefined]
10. take 3 $ filter odd [1, 3, undefined]
Exercise 01¶
[x^y | x <- [1..5], y <- [2, undefined]]
The undefined from the second list will have to be evaluated as it is used as the exponent and this expression will return ⊥.
Exercise 02¶
take 1 $ [x^y | x <- [1..5], y <- [2, undefined]]
It will return the result of 1 ^ 2 and not ⊥.
This is because of take 1 which will require the evaluation of the first pair only, not allowing evaluation to reach the undefined.
Because it is a list comprehension, it returns 1 ^ 2 (which is 1) inside a list, so the result is actually [1].
Exercise 03¶
sum [1, undefined, 3]
Returns ⊥ because sum forces the values.
Exercise 04¶
length [1, 2, undefined]
Produces 3.
length only evals the spine, not forcing the values.
Exercise 05¶
length $ [1, 2, 3] ++ undefined
Produces ⊥.
Because of ++ undefined, that undefined is part of the spine, and length needs to evaluate the spine.
NOTE: Of course, if we place that undefined in a value position (rather than in a spine position), then all is fine for length:
λ> length $ [1, 2, 3] ++ [undefined]
4
Exercise 06¶
take 1 $ filter even [1, 2, 3, undefined]
Because of take 1, we’ll stop as soon as we find the even number 2 and we won’t reach undefined.
The result is [2].
Exercise 07¶
take 1 $ filter even [1, 3, undefined]
Even though we have take 1, we don’t find an even number until we reach undefined, and even will force the value to check of its “evenness”, thus causing ⊥ to occur.
Exercise 08¶
take 1 $ filter odd [1, 3, undefined]
An odd number is found before reaching undefined.
The result is [1].
Exercise 09¶
take 2 $ filter odd [1, 3, undefined]
Two odd numbers are found just before reaching undefined.
The result is [1, 3].
Exercise 10¶
take 3 $ filter odd [1, 3, undefined]
Two odd numbers are found, but not the third before reaching undefined, causing ⊥ to occur.
Is it in normal form?¶
Page 494.
For each expression below, determine whether it’s in:
Normal form, which implies weak head normal form.
Weak head normal form only.
Neither.
Remember that an expression cannot be in normal form or weak head normal form if the outermost part of the expression isn’t a data constructor. It can’t be in normal form if any part of the expression is unevaluated.
NOTE: The _ symbol in the examples below mean a value or expression has not been evaluated.
Exercise 01¶
[1, 2, 3, 4, 5]
NF and WHNF.
NF because no expression or sub-expression is un-evaluated. WHNF because it is evaluated to at least the first/outermost data constructor (and by definition, anything in NF is also in WHNF).
Exercise 02¶
1 : 2 : 3 : 4 : _
WHNF.
Not all expressions have been evaluated due to the _ symbol.
Exercise 03¶
enumFromTo 1 10
Neither because it is a function application to all possible arguments.
Exercise 04¶
length [1, 2, 3, 4, 5]
Neither. It is a function application.
Exercise 05¶
sum (enumFromTo 1 10)
Neither. It is a function application, which results in a value, which is also applied to a function.
Exercise 06¶
['a'..'m'] ++ ['n'..'z']
Neither.
The outermost part is a function application of ++.
Exercise 07¶
(_, 'b')
WHNF.
The outermost part is the data constructor (,) even though not all sub-expressions are fully evaluated.
To be clear here what’s super important is recognizing that WHNF and NF are syntactic properties of expressions And in particular it’s very easy to find out if an expression is in WHNF Neither are properties of the values denoted by those expressions
More Bottoms¶
Page 504.
Exercise 01¶
take 1 $ map (+1) [undefined, 2, 3]
Will be ⊥ because the first element we try to take and force is undefined, which is bottom.
Exercise 02¶
take 1 $ map (+1) [1, undefined, 3]
Yes,m it will return [2] from the evaluation of (+ 1) 1. We take 1 element before having to reach and try to force undefined.
Exercise 03¶
take 2 $ map (+1) [1, undefined, 3]
No, it will be ⊥ because we try have to force two elements from the list, and the second one is undefined.

Note the part in red. It was able to evaluate at least the first value, but reached bottom when trying the second one.
Exercise 04¶
What does the following mystery function do? What is its type? Describe it (to yourself or a loved one) in standard English and then test it out in the REPL to make sure you are correct.
itIsMystery xs = map (\x -> elem x "aeiou") xs
It returns a list of Bool.
True if the current element is a lowercase vowel, False otherwise.
It’s type is [Char] -> [Bool].
λ> isMistery "hello"
[False,True,False,False,True]
λ> isMistery "abcde"
[True,False,False,False,True]
Exercise 05¶
What will be the result of the following functions:
a. map (^2) [1..10]
b. map minimum [[1..10], [10..20], [20..30]] (n.b. minimum is not the same function ass the min function that we used before)
c. map sum [[1..5], [1..5], [1..5]]
a¶
Each element in the list will be raised to the second power:
λ> map (^ 2) [1 .. 10]
[1,4,9,16,25,36,49,64,81,100]
b¶
It will return a list with the smallest (minimum) value of each sub-list.
λ> minimum [1 .. 10]
1
λ> minimum [10 .. 20]
10
λ> minimum [20 .. 30]
20
λ> map minimum [[1 .. 10], [10 .. 20], [20 .. 30]]
[1,10,20]
c¶
It will return a list with three elements which sums [1 .. 5] in each case.
λ> map sum [[1 .. 5], [1 .. 5], [1 .. 5]]
[15,15,15]
Exercise 06¶
Back in Chapter 7, you wrote a function called foldBool. That function exists in a module known as Data.Bool and is called bool. Write a function that does the same (or similar, if you wish) as the map if-then-else function you saw above but uses bool instead of the if-then-else syntax. Your first step should be bringing the bool function into scope by typing import Data. Bool at your REPL prompt.
This is the “map if-then-else function we saw above”:
λ> map (\x -> if x == 3 then (- x) else x) [1 .. 10]
[1,2,-3,4,5,6,7,8,9,10]
First, here’s how bool from Data.Bool works:
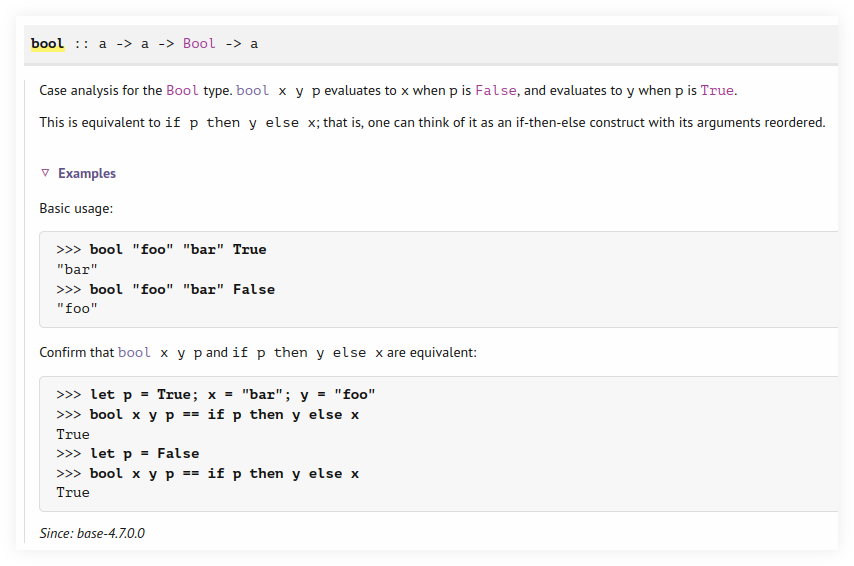
It takes an argument of type \(a\) and another argument of type \(a\) and a Bool.
If the Bool is False, return the first argument; else return the second argument.
λ> import Data.Bool (bool)
λ> :type bool
bool :: a -> a -> Bool -> a
λ> bool "Lara" "Croft" False
"Lara"
λ> bool "Lara" "Croft" True
"Croft"
λ> if not False then "Lara" else "Croft"
"Lara"
λ> if False then "Lara" else "Croft"
"Croft"
So, the solution:
import Data.Bool (bool)
λ> map (\n -> bool n (- n) (n == 3)) [1 .. 5]
[1,2,-3,4,5]
n is the current number.
If n == 3 is False, simply return n.
But if n == 3 is True, then negate n.
Exercises: Filtering¶
Page 335.
Exercise 1¶
How might we write a filter function that would give us all the multiples of 3 out of a list from 1 to 30?
A multiple of 3 is a number whose remainder of it by 3 is 0.
One approach is to make a tiny helper function to check if a number is a multiple of three and then use it in the “main” function.
isMultipleOf3 :: Int -> Bool
isMultipleOf3 n = rem n 3 == 0
λ> filter isMultipleOf3 [1 .. 30]
[3,6,9,12,15,18,21,24,27,30]
Exercise 2¶
Recalling what we learned about function composition, how could we compose the above function with the length function to tell us how many multiples of 3 there are between 1 and 30?
isMultipleOf3 :: Int -> Bool
isMultipleOf3 n = rem n 3 == 0
countMultiplesOf3 :: [Int] -> Int
countMultiplesOf3 = length . filter isMultipleOf3
Of course, we’d rather do it more abstract and reusable:
--
-- Checks whether y is a multiple of x.
--
isMultipleOf :: Integer -> Integer -> Bool
isMultipleOf x y = rem y x == 0
countMultiplesOf :: Integer -> [Integer] -> Int
countMultiplesOf n = length . filter (isMultipleOf n)
λ> countMultiplesOf 3 [1 .. 30]
10
λ> countMultiplesOf 5 [1 .. 30]
6
λ> countMultiplesOf 10 [1 .. 30]
3
Exercise 3¶
Next, we’re going to work on removing all articles (“the,” “a,” and “an”) from sentences. You want to get to something that works like this:
λ> myFilter "the brown dog was a goof"
["brown","dog","was","goof"]
Let’s assume these three string examples:
snake :: [Char]
snake = "there a snake in here"
fruit :: [Char]
fuit = "an apple is a fruit"
jedi :: [Char]
jedi = "may the force be with you"
Solution 1¶
One approach is maybe create a tiny isArticle function that is then used in the “main” function:
--
-- ASSUME: The input is all in lower case.
--
isArticle :: [Char] -> Bool
isArticle word = word == "a" || word == "an" || wrod "the"
--
-- ASSUME: The input is all in lowercase.
--
dropArticles :: [Char] -> [[Char]]
dropArticles str = filter (not . isArticle) (words str)
Note the not . isArticle composition.
λ> dropArticles snake
["there","snake","here"]
λ> dropArticles fruit
["apple","is","fruit"]
λ> dropArticles jedi
["may","force","be","with","you"]
Hint
The type [Char] -> [[Char] is the same as String -> [String].
Solution 2¶
Another approach is to do it all at once in the same function:
dropArticles :: [Char] -> [[Char]]
dropArticles = filter (\s -> not . elem s $ ["a", "an", "the"]) . words
First split the string into individual words and then drop it if it is not “a”, “an” or “the”.
Function composition and point-free style were used for this solution
and also the application operator $.
And instead of not . elem, let’s remember that notElem exists in
Prelude:
dropArticles :: [Char] -> [[Char]]
dropArticles = filter (\s -> notElem s $ ["a", "an", "the"]) . words
Zipping exercises¶
Page 337.
Exercise 1¶
Write your own version of zip, and ensure it behaves the same as the original:
zip :: [a] -> [b] -> [(a, b)]
zip = undefined
Solution 1¶
myZip :: [a] -> [b] -> [(a, b)]
myZip [] _ = []
myZip _ [] = []
myZip (x : xs) (y : ys) = (:) (x, y) $ myZip xs ys
Pattern matching and the cons operator.
The application operator $ is used too, and it is possible because the cons operator : was placed in prefix position.
We could also use parentheses instead of $:
... = (:) (x, y) (myZip xs ys)
And use the cons in infix position:
... = (x, y) : (myZip xs ys)
Solution 2¶
Using the go function pattern, which allows us to use tail call recursion:
myZip :: [a] -> [b] -> [(a, b)]
myZip xs ys = go xs ys []
where
go :: [a] -> [b] -> [(a, b)] -> [(a, b)]
go [] _ acc = acc
go _ [] acc = acc
go (x : lox) (y : loy) acc = go lox loy (acc ++ [(x, y)])
Note how an accumulator was introduced so the consing of the list happens at the last position, thus enabling TCO.
Also, we do acc ++ [(x, y)] rather than [(x, y)] ++ acc, because we want to append to the accumulator, not prepend to it.
Exercise 2¶
Do what you did for zip but now for zipWith:
zipWith :: (a -> b -> c) -> [a] -> [b] -> [c]
zipWith = undefined
Solution 1¶
myZipWith :: (a -> b -> c) -> [] a -> [] b -> [] c
myZipWith _ [] _ = []
myZipWith _ _ [] = []
myZipWith f (x : xs) (y : ys) = [f x y] ++ (myZipWith f xs ys)
Because we are NOT doing tail call in this solution, we do [f x y] ++ “the rest of the recursion”.
Solution 2¶
Using the go function pattern and tail call optimization.
myZipWith :: (a -> b -> c) -> [a] -> [b] -> [c]
myZipWith f xs ys = go f xs ys []
where
go :: (a -> b -> c) -> [a] -> [b] -> [c] -> [c]
go _ [] _ acc = acc
go _ _ [] acc = acc
go fn (x : lox) (y : loy) acc = go fn lox loy (acc ++ [(fn x y)])
Because we are doing TCO, we do acc ++ [(fn x y)].
The accumulator always has the latest computation thus far.
With TCO, we are not just storing expressions that will be evaluated later, in the unwinding phase of the execution.
So, if we do (f x) ++ rest or acc ++ (f x) depends on the type of recursion we are doing.
Exercise 3¶
Rewrite your zip in terms of the zipWith you wrote.
Solution 1¶
Well, zip must create a tuple, and to create a tuple we use the tuple constructor (,).
zipWith takes a function.
We can simply partially apply myZipWith to (,) and we are done!
myZip :: [a] -> [b] -> [(a, b)]
myZip = myZipWith (,)
λ> myZip [1, 2] "ab"
[(1,'a'),(2,'b')]
We also made myZip point-free.
Chapter exercises¶
Page 338.
NOTE: We’ll need to import functions from Data.Char.
Data.Char¶
Exercise 1¶
Query the types of isUpper and toUpper.
Solution¶
λ> import Data.Char (isUpper, isLower)
λ> :type isUpper
isUpper :: Char -> Bool
λ> :type isLower
isLower :: Char -> Bool
Exercise 2¶
Given the following behaviors, which would we use to write a function that filters all the uppercase letters out of a String?
λ> isUpper 'J'
True
λ> toUpper 'j'
'J'
Write that function such that, given the input "HbEfLrLxO", your function will return "HELLO".
Which function?¶
If we want to filter all uppercase letters, it means we want to ignore the lowercase letters.
We could use not . isLower, but simpler yet is to simply use isUpper.
Also, we don’t to transform a letter to uppercase, but just check if it is uppercase.
Thus, we use isUpper instead of toUpper.
Solution 1¶
Idiomatic approach making use of stdfn filter and simply partially applying it to isUpper.
We also use point-free style.
import Data.Char (isUpper)
onlyUppers :: [Char] -> [Char]
onlyUppers = filter isUpper
--
-- λ> onlyUppers "HbEfLrLxO"
-- "HELLO"
--
Solution 2¶
Pattern matching, go function approach, and manually accumulating the uppercase letters.
import Data.Char (isUpper)
onlyUppers :: [Char] -> [Char]
onlyUppers str = go str []
where
go :: [Char] -> [Char] -> [Char]
go [] loc = loc
go (c : cs) loc =
if isUpper c
then go cs (c : loc)
else go cs loc
Exercise 3¶
Write a function that will capitalize the first letter of a string and return the entire string. For example, if given the argument “julie”, it will return “Julie”.
Solution¶
Pattern match on the first char and the rest of the string uppercase the first char and cons it to the rest of the unmodified string.
import Data.Char (toUpper)
--
-- ASSUME: The input has length >= 1.
--
capitalize :: [Char] -> [Char]
capitalize [] = ""
capitalize (c : cs) = toUpper c : cs
--
-- λ> capitalize "yoda"
-- "Yoda"
--
-- λ> capitalize "ahsoka tano"
-- "Ahsoka tano"
--
Exercise 4¶
Now make a new version of that function that is recursive, such that if you give it the input “woot”, it will holler back at you “WOOT”. The type signature won’t change, but you will want to add a base case.
Solution 1¶
Pattern matching and the cons operator :.
import Data.Char (toUpper)
capitalizeAll :: [Char] -> [Char]
capitalizeAll [] = ""
capitalizeAll (c : cs) = toUpper c : capitalizeAll cs
--
-- λ> capitalizeAll "https"
-- "HTTPS"
--
Solution 2¶
Point-free style using foldr (not yet learned in the book at this point) and function composition.
import Data.Char (toUpper)
capitalizeAll :: [Char] -> [Char]
capitalizeAll = foldr ((:) . toUpper) ""
: cons is composed with toUpper.
Each character is then uppercased and consed onto the accumulator, producing the final all-uppercase string result.
Exercise 5¶
To do the final exercise in this section, we’ll need another standard function for lists called head. Query the type of head, and experiment with it to see what it does. Now write a function that will capitalize the first letter of a String and return only that letter as the result.
λ> :type head
head :: [a] -> a
Solution 1¶
The $ ‘infixr 0’ function application operator causes head to be applied to str first.
That result is then the argument to toUpper.
capitalizeFirst :: [Char] -> Char
capitalizeFirst str = toUpper $ head str
Exercise 6¶
Solution 1¶
Point-free, function composition.
head returns the first char of the string which toUpper is then applied.
capitalizeFirst :: [Char] -> Char
capitalizeFirst = toUpper . head
--
-- λ> capitalizeFirst "haskell"
-- 'H'
--
Ciphers¶
Basically, do a rightwards Caesar shift.
Let’s consider lowercase-only English alphabet letters.
Solution 1 (baby steps 😅)¶
We’ll go with an approach where we map each letter from ‘a’ to ‘z’ to ints from 0 to 25. So ‘a’ is 0 and ‘z’ is 25.
Recall that ‘a’ is 97 in both ASCII and UTF-8.
Let’s name our 97 as a:
a :: Int
a = 97
The English alphabet has 26 letters:
λ> length ['a' .. 'z']
26
That means we need to “wrap around” at 26.
That will be one of our parameters to the mod function:
λ> mod 0 26
0
λ> mod 1 26
1
λ> mod 25 26
25
λ> mod 26 26
0
λ> mod 27 26
1
Consider ‘z’, which is 25 in our 0 to 25 mapping.
If we want to shift ‘z’ rightwards by 1 position, we’ll do \(25 + 1 = 26\), and mod 26 26 is 0, which is the position for ‘a’.
Then, \(0 + 97 = 97\), and ord 97 is ‘a’. \(1 + 97 = 98\), and ord 98 is ‘b’.
By adding 97 to our ints, we can compute the int value of each one of the letters from 0 to 25.
Play with those ideas in GHCi’s REPL to get a better feeling for it.
module Cipher1 where
import Data.Char (chr, ord)
--
-- The int value of 'a' in ASCII and UTF-8 is 97.
--
a :: Int
a = 97
--
-- Because the English alphabet contains 26 letters, this is the
-- number we need to “wrap around” when shifting char positions.
--
wrp :: Int
wrp = 26
--
-- Translates the zero-based position of a character `c` in the
-- lowercase English alphabet into its corresponding 0 to 25 numeric
-- mapping.
--
-- Examples:
-- • ‘a’ → 0
-- • ‘z’ → 25
--
toPos :: Char -> Int
toPos c = ord c - a
--
-- Translates the zero-based position `i` into its corresponding
-- lowercase letter in the English Alphabet.
--
-- Examples:
-- • 0 → ‘a’
-- • 25 → ‘z’
--
toChr :: Int -> Char
toChr i = chr $ i + a
--
-- Right-shifts c by n positions.
--
-- Examples:
--
-- • move 1 'a' → 'b'
-- • move 3 'a' → 'd'
-- • move 1 'z' → 'a'
-- • move 3 'z' → 'c'
--
move :: Int -> Char -> Char
move n c = toChr $ mod (toPos c + n) wrp
--
-- Applies the Caesar to `chrs` by shifting each letter `n` positions
-- to the right.
--
-- ASSUME: Lowercase-only English alphabet letters.
--
caesar :: Int -> [Char] -> [Char]
caesar n chrs = map (move n) chrs
Then, on a GHCi session, we can test try it:
λ> caesar 3 "xyz"
"abc"
λ> caesar 1 "abc"
"bcd"
λ> caesar 3 "abc"
"def"
λ> caesar 1 "xyz"
"yza"
λ> caesar 3 "xyz"
"abc"
We could make caesar take only the n param and leave the chrs argument to map point free:
caesar :: Int -> [Char] -> [Char]
caesar n = map (move n)
Other changes like partially applying move to n would also be possible, but this is good enough.
Solution 2¶
Currently, move can only shift chars to the right.
How can we make move able to shift characters to the right and to the left as well?
If we find a solution for this, we would also be able to do the unCaesar function asked in the book.
This is the current implementation:
--
-- Right-shifts c by n positions.
--
-- Examples:
--
-- • move 1 'a' → 'b'
-- • move 3 'a' → 'd'
-- • move 1 'z' → 'a'
-- • move 3 'z' → 'c'
--
move :: Int -> Char -> Char
move n c = toChr $ mod (toPos c + n) wrp
Hmm… We are always using + to add (shift to the right).
If we can improve move so that it takes the function + or - as parameter, then it would be able to shift chars left and right.
Let’s try this:
--
-- Shifts `c` by `n` positions left or right according to `f`.
--
-- Examples:
--
-- • move (+) 3 'z' → 'c'
-- • move (-) 3 'a' → 'x'
--
move :: (Int -> Int -> Int) -> Int -> Char -> Char
move f n c = toChr $ mod (f (toPos c) n) wrp
And a in GHCi:
λ> move (+) 1 'z'
'a'
λ> move (-) 1 'a'
'z
And let’s also update caesar:
--
-- Applies the Caesar to `chrs` by shifting each letter `n` positions
-- to the right or left according to `f`.
--
-- ASSUME: Lowercase-only English alphabet letters.
--
caesar :: (Int -> Int -> Int) -> Int -> [Char] -> [Char]
caesar f n = map (move f n)
Which then works like this:
λ> caesar (+) 3 "xyz"
"abc"
λ> caesar (-) 3 "abc"
"xyz"
That is cool and all and all this FP trickery! Nice to practice and learn, but it so happens that our original version was already taking are of left and right shifts.
Solution 3¶
Our original move function was already able to take care of _both left and right shifting:
move :: Int -> Char -> Char
move n c = toChr $ mod (toPos c + n) wrp
Even though it uses (+) exclusively, if we pass it a negative n, it actually subtracts n from the result of toPos c.
Isn’t math a lot of fun‽
λ> 1 + (-3)
-2
λ> toPos 'a'
0
λ> toPos 'a' + (-3)
-3
λ> move (-1) 'z'
'y'
λ> move (-1) 'a'
'z'
So, let’s just update our doc comments and the examples and call it a day!
module Cipher3 where
import Data.Char (chr, ord)
--
-- The int value of 'a' in ASCII and UTF-8 is 97.
--
a :: Int
a = 97
--
-- Because the English alphabet contains 26 letters, this is the
-- number we need to “wrap around” when shifting char positions.
--
wrp :: Int
wrp = 26
--
-- Translates the zero-based position of a character `c` in the
-- lowercase English alphabet into its corresponding 0 to 25 numeric
-- mapping.
--
-- Examples:
-- • ‘a’ → 0
-- • ‘z’ → 25
--
toPos :: Char -> Int
toPos c = ord c - a
--
-- Translates the zero-based position `i` into its corresponding
-- lowercase letter in the English Alphabet.
--
-- Examples:
-- • 0 → ‘a’
-- • 25 → ‘z’
--
toChr :: Int -> Char
toChr i = chr $ i + a
--
-- Shifts `c` by `n` positions left or right according to `n` being
-- positive or negative!
--
-- Examples:
--
-- • move 1 'a' → 'b'
-- • move (-1) 'a' → 'z'
-- • move 3 'z' → 'c'
-- • move (-3) 'a' → 'x'
--
move :: Int -> Char -> Char
move n c = toChr $ mod (toPos c + n) wrp
--
-- Applies the Caesar to `chrs` by shifting each letter `n` positions
-- to the right if `n` is positive; to the left if `n` is negative.
--
-- ASSUME: Lowercase-only English alphabet letters.
--
caesar :: Int -> [Char] -> [Char]
caesar n = map (move n)
--
-- λ> caesar 3 "abc"
-- "def"
--
-- λ> caesar 3 "xyz"
-- "abc"
--
-- λ> caesar (-3) "abc"
-- "xyz"
--
-- λ> caesar (-3) "xyz"
-- "uvw"
--
Solution 4¶
So our caesar implementation is able to encrypt and decrypt messages just by virtue of the n param being positive or negative.
But the book mentions we should create both caesar and the unCaesar functions.
caesar :: Int -> [Char] -> [Char]
caesar n = map (move $ abs n)
unCaesar :: Int -> [Char] -> [Char]
unCaesar n = map (move (negate . abs $ n))
We use abs and negate to prevent caesar and unCaesar to work incorrectly in case users pass a negative int, as these two functions will now each work to shift chars to the right or left directions respectively.
This fourth solution is not much better than the third one where caesar alone was able to encrypt and decrypt messages solely based on n being positive or negative.
Writing your own standard functions¶
myAnd¶
myAnd :: [Bool] -> Bool
myAnd [] = True
myAnd (b : bs) = case b of
False -> False
_ -> myAnd bs
Linter suggests rewriting using if then else syntax:
myAnd :: [Bool] -> Bool
myAnd [] = True
myAnd (b : bs) = if b then myAnd bs else False
Which in turn complains if is redundant, and && should be used instead:
myAnd :: [Bool] -> Bool
myAnd [] = True
myAnd (b : bs) = b && myAnd bs
And using foldr (which we didn’t learn yet in the book):
myAnd :: [Bool] -> Bool
myAnd bs = foldr (&&) True bs
And it is possible to make it point-free:
myAnd :: [Bool] -> Bool
myAnd = foldr (&&) True
myOr¶
We could do as with myAnd and try different implementations, but let’s stick to this one:
myOr :: [Bool] -> Bool
myOr [] = False
myOr (b : bs) = b || myOr bs
Note that for myAnd, the base case for the empty list is True, whereas for myOr, the base case for the empty list is False.
myAny¶
myAny :: (a -> Bool) -> [a] -> Bool
myAny _ [] = False
myAny f (x : xs) = f x || myAny f xs
--
-- λ> myAny even [1, 3, 4, 5]
-- True
--
myElem¶
First the recursive approach:
myElem :: Eq a => a -> [a] -> Bool
myElem _ [] = False
myElem e (x : xs) = (==) e x || myElem e xs
Then using myAny:
myElem :: Eq a => a -> [a] -> Bool
myElem e = myAny (e ==)
--
-- λ> myElem 3 [1, 5, 9]
-- False
--
-- λ> myElem 3 [1, 5, 3, 9]
-- True
--
Point-free on the list element (we don’t do myElem e xs, but myElem e).
And we do sectioning and partial application of == to e.
myReverse¶
Get x from the head of the list, and concatenate it to the end :)
We put it (the x) inside brackets to make a list out of it, as ++ concatenates lists (both operands must be lists).
myRev :: [a] -> [a]
myRev [] = []
myRev (x : xs) = myRev xs ++ [x]
--
-- λ> myRev "xyz"
-- "zyx"
--
squish¶
squish :: [[a]] -> [a]
squish [] = []
squish (xs : xss) = xs ++ squish xss
--
-- λ> squish [[1], [2], [3]]
-- [1,2,3]
--
Or using foldr and point-free style (not specifying the xss param):
squish :: [[a]] -> [a]
squish = foldr (++) []
squishMap¶
NOTE: squishMap is just like concatMap from Data.Foldable.
squishMap :: (a -> [b]) -> [a] -> [b]
squishMap _ [] = []
squishMap f (xs : xss) = f xs ++ squishMap f xss
--
-- λ> squishMap (\x -> [1, x, 3]) [2]
-- [1,2,3]
--
-- λ> squishMap (\x -> [x + 1]) [1, 2, 3]
-- [2,3,4]
--
Or reusing squish and function composition with map.
Point-free as the list parameter is not explicitly specified.
squishMap :: (a -> [b]) -> [a] -> [b]
squishMap f = squish . map f
To try to understand it better, look at this:
λ> map (\n -> [1, n, 3]) [2]
[[1,2,3]]
map itself returns a list, and the lambda is returning a list of its own, thus the result the list returned by the lambda contained inside of the list returned by map.
Then squish flattens it to a single-level list.
squishAgain¶
squishAgain :: [[a]] -> [a]
squishAgain = squishMap id
--
-- λ> squishAgain [[1], [2], [3]]
-- [1,2,3]
--
id simply returns the argument given to it, and our squishAgain is supposed to simply flatten a list of lists.
Because we are asked to use squishMap which requires a function as its first arg, but we don’t want to transform each inner list in any way, we then simply give it id.
myMaximumBy¶
λ> import Data.Foldable (maximumBy)
λ> :type maximumBy
maximumBy :: Foldable t => (a -> a -> Ordering) -> t a -> a
λ> maximumBy compare []
*** Exception: maximumBy: empty structure
Note that maximumBy is not defined for empty lists.
For now, we can consider Folable t to be a list of t [t].
Solution 1¶
myMaximumBy :: (a -> a -> Ordering) -> [a] -> a
myMaximumBy f xs = go f (tail xs) (head xs)
where
go :: (a -> a -> Ordering) -> [a] -> a -> a
go _ [] winner = winner
go fn (h : lst) winner =
case fn h winner of
GT -> go fn lst h
_ -> go fn lst winner
Using the go function pattern, start by considering the head of the list to be the maximum so far, keep go recurring with either the current maximum so far or the new maximum value.
Solution 2¶
NOTE: There is a Discord thread on this solution.
myMaximumBy :: (a -> a -> Ordering) -> [a] -> a
myMaximumBy _ [x] = x
myMaximumBy f (x : xs) =
case f x g of
LT -> g
_ -> x
where g = myMaximumBy f xs
g is the result of applying myMaximumBy to f and xs, but here xs is actually the tail of the list (because of (x : xs) pattern matching).
It will build expressions up to a point where the list is composed of a single element, when it pattern matches on _ [x].
From there, it can finally “unwind” and evaluate the built expressions.
And because of those things, it will actually compare backwards.
Let’s rename myMaximumBy to mmb, inline g, rename x and xs to h and rest respectively, make f an alias to compare, and try to visualize what is going on.
mmb :: (a -> a -> Ordering) -> [a] -> a
mmb _ [n] = n
mmb f (h : rest) =
case f h (mmb f rest) of
LT -> mmb f rest
_ -> h
Apply mmb to f and [3, 2, 4, 1].
h is 3 and rest is [2, 4, 1].
mmb f (2 : [3, 4, 1])
case f 2 (mmb f [3, 4, 1]) of
LT -> mmb f [3, 4, 1]
_ -> 2
We yet don’t know what is the result of case f 3 (mmb f [2, 4, 1]) of, so we have to evaluate it.
Our new h is 3 and the new rest is [4, 1].
mmb f (2 : [4, 1])
case f 2 (mmb f [4, 1]) of
LT -> mmb f [4, 1]
_ -> 2
We yet don’t know what is the result of case f 2 (mmb f [4, 1]) of, so we have to evaluate it.
Our new h is 4 and the new rest is [1].
mmb f (4 : [1])
case f 4 (mmb f [1]) of
LT -> mmb f [1]
_ -> 4
At this point, we call mmb f [1], which will finally cause _ [n] pattern to match, and return 1.
We finally have two numeric values to compare in case of and start “unwinding” the expressions.
The case ... of will now compare 4 and 1, and 4 is the winner.
Then 4 and 2, an 4 is still the winner.
Then 4 and 3, and 4 is still the winner.
What about we try with [1, 5, 3, 4, 2]?
Remember our case ... of:
case f h (mmb f rest) of
LT -> mmb f rest
_ -> h
Then:
case f 1 (mmb f [5, 3, 4, 2])
case f 5 (mmb f [3, 4, 2])
case f 3 (mmb f [4, 2])
case f 4 (mmb f [2])
case f 4 2 ⇒ 4
case f 3 4 ⇒ 4
case f 5 4 ⇒ 5
case f 1 5 ⇒ 5